Quantum Computing basics with Q# – The superposition of a qubit

There are some problems so difficult, so incredibly vast, that even if every supercomputer in the world worked on the problem, it would still take longer than the lifetime of the universe to solve!
The phrase above, found in Microsoft Docs, captures today’s problems with our regular computers and as a result the limitations we face in our every day lives. Numerous problems in environment, health, agriculture and many other fields have a solution lost in a vast ocean of possible answers that need to be tested one by one for correctness.
Enters Quantum Computing!
What is Quantum Computing
Quantum computing is the use of quantum-mechanical phenomena such as superposition and entanglement to perform computations. These quantum-mechanical phenomena are described by quantum physics as the behavior of atoms and fundamental particles, like electrons and photons. A quantum computer operates by controlling the behavior of these particles, but in a way that is completely different from regular computers. Quantum computers are vastly more capable of solving problems like integer factorization (which underlies RSA encryption), but since they are notoriously difficult to build and program they are crippled by errors in such a degree, that their operation falls apart before any nontrivial program has a chance to complete.
What is Quantum Superposition
Imagine two colliding waves in the sea; sometimes they perfectly add to make a bigger wave, sometimes they completely cancel each other out, but often it’s just a combination of both somewhere in between. This constructive or destructive interference of waves is known as superposition in classical physics.
In Quantum mechanics though, superposition can be a bit weirder!
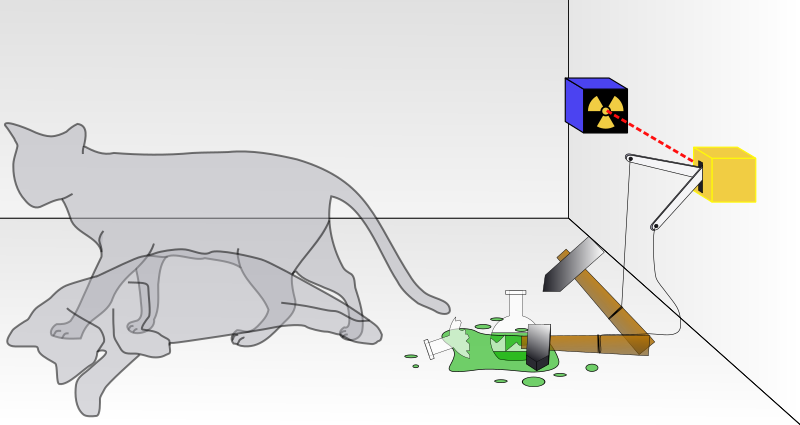
Particles that exist in different states (for example in different positions or moving at different speeds, etc) are thought of as existing across all the possible states at the same time! Yes, a particle in superposition can exist in two places at the same time and/or move at different speeds simultaneously. This “unnatural” state of matter, practically impossible for a human brain to comprehend, it’s one of the weirdest realities of quantum physics.
The famous thought experiment, Schrödinger’s cat, was an attempt to illustrate the problems of Copenhagen interpretation of quantum mechanics by applying quantum mechanics to everyday objects. Copenhagen interpretation, devised somewhere around 1926, was stating that physical systems, in general, do not have a state until measured.
However, this weird behavior becomes human-friendly once a measurement of a particle is made; when for example we check its position, no matter how we checked it, the superposition is lost and the particle exists in one known state.
What is Quantum entanglement
Quantum entanglement that Einstein described as “spooky action over distance”, is a relationship between fundamental particle properties that persist over distance without requiring transmission of information.

Imagine for example, that we put each member of a pair of gloves in boxes (somehow without seeing them) and mail one of them to the opposite side of the earth. Whoever is the recipient should be able, by looking inside her/his box, to determine the properties of the glove that we still have with us in our box. If she/he states “it’s blue” and we open our box our glove will be blue. Simple and not that spooky at all, right? But what about, if the recipient throws the box in green paint affecting the glove’s color. Will that make my glove change color too? In the particle world, yes. My glove will instantly be green…!
In other words, measurements of physical properties such as position, momentum, spin, and polarization performed on entangled particles are found to be perfectly correlated, even when the particles are separated by a large distance. Measurements on one particle, affect the entangled system as a whole.
Quantum programming with Q#
Quantum programming is the process of assembling sequences of instructions, called quantum programs, that are capable of running on a quantum computer. Quantum programming languages help express quantum algorithms using high-level constructs. High-end programming languages, like Q#, use Quantum software development kits, that provide the means to simulate a quantum environment.
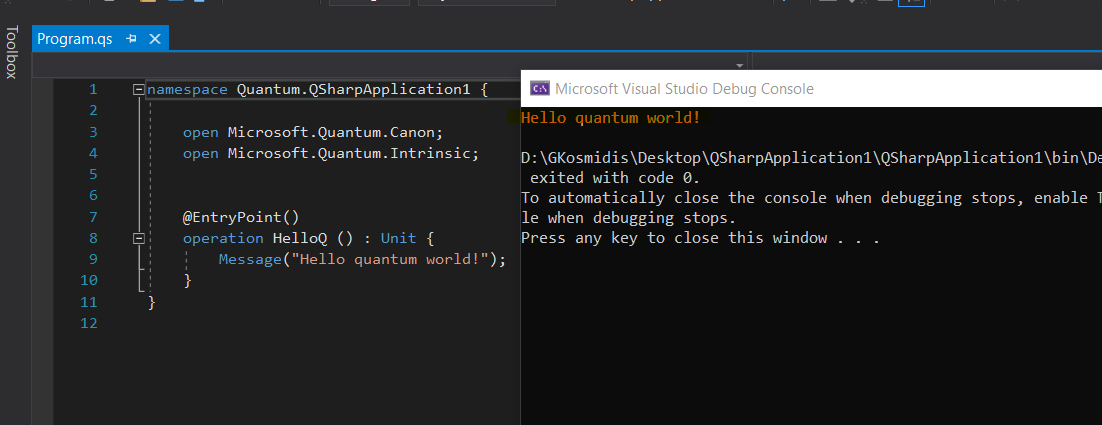
Hello Quantum World!
Q# is built to play well with .NET languages such as C# and F#; we just need to install the Quantum Development Kit! In order to do so we need to download and install this Visual Studio Extension: https://marketplace.visualstudio.com/items?itemName=quantum.DevKit.
When the installation is completed, we can start Visual Studio (it has to be v16.3+) and perform the following steps to create a new Q# application:
- Start Visual Studio (v16.3+)
- Click on “Create a new project”
- Type “Q#” in the search box
- Select Q# Application
- Select Next
- Choose a name and location for your application
- Make sure that “place project and solution in same directory” is unchecked
- Select Create
And that’s it! We can now run our app and get the familiar greetings:
Randomly select an atom in the Universe
That is, if all atoms in the universe had an index! What we really going to create is a random number generator with an upper limit bigger than the number of the atoms in the universe. This, not so impressive feat, will perfectly demonstrate the very basics of working with Qubits. This is just a blog post after all, not the full documentation!
The
Intin Q# is a 64-bit signed integer, whereBigIntis a signed integer of arbitrary size and it’s based onBigInteger. Read more about the The Type Model.
The most interesting type in Q#, the Qubit, upgrades the bit we know to mythical proportions! Where classical bits hold a single binary value such as 0 or 1, the state of a qubit can be in a superposition of 0 and 1! Conceptually, a qubit can be thought of as a direction in space (also known as a vector), where a qubit can be in any of the possible directions. The two classical states are the two directions on one axes (e.g. x’x); representing 100% chance of measuring 0 and 100% chance of measuring 1. This representation is also more formally visualized by the bloch sphere.
As a first step, let’s try to allocate a qubit, set it to superposition and then measure the result. This will give us, after the measurement, either 100% of the times 1 or 100% of the times 0; while in superposition though it has exactly 50% chances of being either 0 or 1:
operation GetRandomResult() : Result {
using (q = Qubit()) { // Allocate a qubit.
H(q); // Hadamard operation; put the qubit to superposition. It now has a 50% chance of being 0 or 1.
return MResetZ(q); // Measure the qubit value in the Z basis, and reset it to the standard basis state |0〉 after;
// MResetX(q) and MResetY(q) do the same for X and Y basis.
}
}An
operationis for quantum operations in quantum data, where afunctionmodified classical data. Learn how to work with them in the Q# Operations and Functions section of the documentation.
MResetZmeasures a single qubit in the Z basis, and resets it to the standard basis state |0〉 following the measurement. Similar operations are theMResetXandMResetY. All the measurement operations are contained in the Microsoft.Quantum.Measurement Q# library.
Since we are talking about 0s and 1s, we need a way to find how many bits represent the max limit requested (for us the number of atoms in the universe). Thankfully, the library Microsoft.Quantum.Math contains a function named BitSizeL which does exactly that for signed integers of arbitrary size (BitSizeI does it for Int). We then need a loop to add to an array of Results the Result returned by the GetRandomResult() method:
mutable bits = new Result[0]; //This is how to declare a mutable variable
let bitSize = BitSizeL(max); //This is how to declare an immutable variable
for (_ in 1..bitSize) { //Loop
let result = GetRandomResult(); //Get the result of GetRandomResult() into the the result variable
set bits += [result]; //Update the array bits, adding at the end the current result
}Almost there! We just need to convert this array of Result to a BigInt. We can do that by first converting the array of Result to an array of bool, and then the array of bool to BigInt:
let randomNumber = BoolArrayAsBigInt(ResultArrayAsBoolArray(bits));All supported conversions are in the Microsoft.Quantum.Convert Q# Library.
There is a problem though! The number of bits that can represent the number requested as max can potentially represent an even bigger number! To compensate for this possible error we can conditionally recurse until we find the correct one:
return randomNumber > max
? SampleRandomNumberInRange(max)
| randomNumber;And finally done! Follows the entire Q# program that returns a really big random number:
namespace Quantum.RandomNumber {
open Microsoft.Quantum.Convert;
open Microsoft.Quantum.Math;
open Microsoft.Quantum.Measurement;
open Microsoft.Quantum.Canon;
open Microsoft.Quantum.Intrinsic;
@EntryPoint()
operation Main () : BigInt {
let max = PowL(10L, 80);
Message($"The lucky atom is number ");
return Generate(max);
}
operation Generate(max : BigInt ) : BigInt {
mutable bits = new Result[0]; //This is how to declare a mutable variable
let bitSize = BitSizeL(max); //This is how to declare an immutable variable
for (_ in 1..bitSize) { //Loop
let result = GetRandomResult(); //Get the result of GetRandomResult() into the the result variable
set bits += [result]; //Update the array bits, adding at the end the current result
}
let sample = BoolArrayAsBigInt(ResultArrayAsBoolArray(bits)); // Convert to BigInt
return sample > max //Check and return if sample is less or equal to max
? Generate(max)
| sample;
}
operation GetRandomResult() : Result {
using (q = Qubit()) { // Allocate a qubit.
H(q); // Hadamard operation; put the qubit to superposition. It now has a 50% chance of being 0 or 1.
return MResetZ(q); // Measure the qubit value in the Z basis, and reset it to the standard basis state |0〉 after;
// MResetX(q) and MResetY(q) do the same for X and Y basis.
}
}
}
Happy coding!
Q# works very well with C#, so it is easy to create a Q# Library and use that library from C# (or F#). An example of this interoperability is the Quantum.RandomNumber solution in my GitHub account!.
Further reading
There are many resources already available that can help you start your journey in the Quantum World. Quantum Katas is a good start to learn by doing, so is the Quantum Teleportation Sample for example can help you understand the quantum entanglement, a way of moving a quantum state from one location to another without having to move physical particle(s) along with it. The entry point for all possible resources is the Microsoft Quantum Documentation.
Conclusion
Physicists have been talking about the power of quantum computing for over 30 years, but the question have always been: will it ever do something useful? Google answered that question just a few months ago, in late 2019, with the Quantum Supremacy experiment that successfully performed a computation in 200 seconds that would otherwise need 10000 years in the faster supercomputer available today! Quantum computing will massively change our lives in so many fields the next years, that it is easily comparable with the invention of the first transistor that led to the 3rd Industrial Revolution, the Digital Revolution. When the first computers appeared, nobody believed that there is going to be a smart phone that will hold more computational power than all the computers of the era combined and we could have that power in our pockets…!


